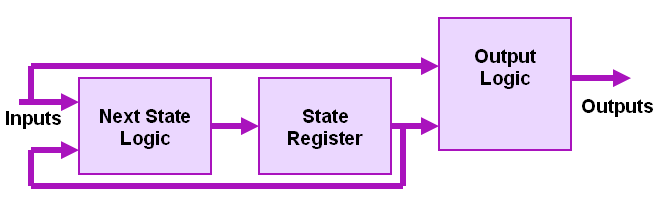
Designing a synchronous finite state machine (FSM) is a common task for a digital logic engineer. A finite state machine can be divided in to two types: Moore and Mealy state machines. Fig. 1 has the general structure for Moore and Fig. 2 has general structure for Mealy. The current state of the machine is stored in the state memory, a set of n flip-flops clocked by a single clock signal (hence “synchronous” state machine). The state vector (also current state, or just state) is the value currently stored by the state memory. The next state of the machine is a function of the state vector in Moore; function of state vector and the inputs in Mealy.
 Fig. 1: Moore State Machine
Fig. 1: Moore State Machine
Fig. 2: Mealy State Machine
Verilog CodingThe logic in a state machine is described using a case statement or the equivalent (e.g., if-else). All possible combinations of current state and inputs are enumerated, and the appropriate values are specified for next state and the outputs. A state machine may be coded as in Code 1 using two separate case statements, or, as in code 2, using only one. A single case statement may be preferred for Mealy machines where the outputs depend on the state transition rather than just the current state.
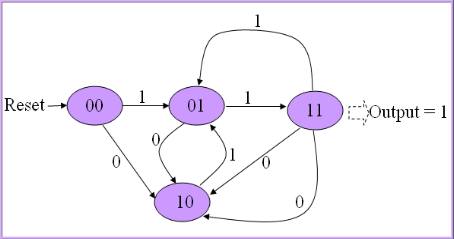
Consider the case of a circuit to detect a pair of 1's or 0's in the single bit input. That is, input will be a series of one's and zero's. If two one's or two zero's comes one after another, output should go high. Otherwise output should be low.
Here is a Moore type state transition diagram for the circuit. When reset, state goes to 00; If input is 1, state will be 01 and if input is 0, state goes to 10. State will be 11 if input repeats. After state 11, goes to 10 state or 01 depending on the inp, since overlapping pair should not be considered. That is, if 111 comes, it should consider only one pair.
Following code the Verilog implementation of the state machine. Note that we updated outp and state in separate always blocks, it will be easy to design. inp is serial input, outp is serial output, clk is clock and rst is asynchronous reset. I have used nonblocking statements for assignments because we use previous state to decide the next state, so state should be registered.
module fsm( clk, rst, inp, outp);
input clk, rst, inp;
output outp;
reg [1:0] state;
reg outp;
always @( posedge clk, posedge rst )
begin
if( rst )
state <= 2'b00;
else
begin
case( state )
2'b00:
begin
if( inp ) state <= 2'b01;
else state <= 2'b10;
end
2'b01:
begin
if( inp ) state <= 2'b11;
else state <= 2'b10;
end
2'b10:
begin
if( inp ) state <= 2'b01;
else state <= 2'b11;
end
2'b11:
begin
if( inp ) state <= 2'b01;
else state <= 2'b10;
end
endcase
end
end
always @(posedge clk, posedge rst)
begin
if( rst )
outp <= 0;
else if( state == 2'b11 )
outp <= 1;
else outp <= 0;
end
endmodule
|
Here is a testbench that can be used to test all these examples. This testbench generates both directed and random test values. We can specify the sequence in the first part.
module fsm_test;
reg clk, rst, inp;
wire outp;
reg[15:0] sequence;
integer i;
fsm dut( clk, rst, inp, outp);
initial
begin
clk = 0;
rst = 1;
sequence = 16'b0101_0111_0111_0010;
#5 rst = 0;
for( i = 0; i <= 15; i = i + 1)
begin
inp = sequence[i];
#2 clk = 1;
#2 clk = 0;
$display("State = ", dut.state, " Input = ", inp, ", Output = ", outp);
end
test2;
end
task test2;
for( i = 0; i <= 15; i = i + 1)
begin
inp = $random % 2;
#2 clk = 1;
#2 clk = 0;
$display("State = ", dut.state, " Input = ", inp, ", Output = ", outp);
end
endtask
endmodule
|
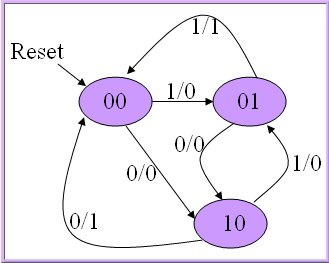
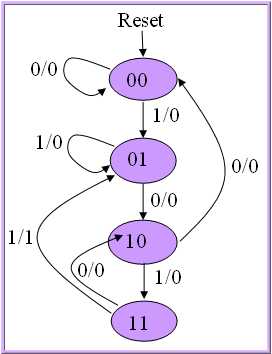
Now, let us re-design the above circuit using Mealy style state machine. Output depends on both state and input. State transition diagram is as follows:
When reset, state becomes idle, that is 00. Next, if 1 comes, state becomes 01 and if 0 comes state becomes 10 with output 0. We have showed input 1, output 0 as 1/0. If input bit repeats, output becomes 1 and state goes to 00.
I implemented this state machine as in the code bellow. Only one always block is used because both outp and state are dependent on state and inp.
module mealy( clk, rst, inp, outp);
input clk, rst, inp;
output outp;
reg [1:0] state;
reg outp;
always @( posedge clk, posedge rst ) begin
if( rst ) begin
state <= 2'b00;
outp <= 0;
end
else begin
case( state )
2'b00: begin
if( inp ) begin
state <= 2'b01;
outp <= 0;
end
else begin
state <= 2'b10;
outp <= 0;
end
end
2'b01: begin
if( inp ) begin
state <= 2'b00;
outp <= 1;
end
else begin
state <= 2'b10;
outp <= 0;
end
end
2'b10: begin
if( inp ) begin
state <= 2'b01;
outp <= 0;
end
else begin
state <= 2'b00;
outp <= 1;
end
end
default: begin
state <= 2'b00;
outp <= 0;
end
endcase
end
end
endmodule
|
Now, let us discuss difference between Moore and Mealy state machines depending on these codes.
Moore state machine is easier to design than Mealy. First design the states depending on the previous state and input. Then design output only depending on state. Whereas in Mealy, you have to consider both state and input while designing the output.
Mealy state machine uses less states than the Moore. Since inputs influence the output in the immediate clock, memory needed to remember the input is less. So, it uses less flip flops and hence circuit is simpler.
In Mealy, output changes immediately when the input changes. We can observe this point when you simulate the codes above. In Moore example, output becomes high in the clock next to the clock in which state goes 11. So, Mealy is faster than Moore. Mealy gives immediate response to input and Moore gives response in the next clock.
Sequence detector:
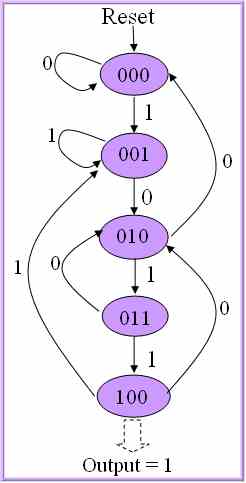
Let us design a circuit to detect a sequence of 1011 in serial input. This is an overlapping sequence. So, if 1011011 comes, sequence is repeated twice. Consider these two circuits. First one is Moore and second one is Mealy. In Moore design below, output goes high only if state is 100. Note that we have used 1 less state than Mealy and hence one flip flop less will be enough to design state machine.
This time I will try to implement only Mealy machine. Try to understand the state diagram and compare them first.
When reset, state goes to 00, where there is no previous inputs. State remains same until we get a '1' in the input since there is no possibility of start of sequence. If a 1 comes in the input, it may be start of sequence, so go to state 01. From 01, if again 1 comes, that means sequence is broken. But there is a possibility of start of another new sequence. So, 01 is start of sequence and stay in the same state. If zero comes, go to state 10.
Another 0 when state is 10 breaks the sequence and state goes to 00, no sequence. If 1 comes, continue to next state 11.
If again 1 comes, sequence completes. Make the output high and go to state 01, because there may be a overlapping sequence as I mentioned earlier. If zero comes, sequence breaks and state goes to 10 since it may be second bit of another sequence.
module m1011( clk, rst, inp, outp);
input clk, rst, inp;
output outp;
reg [1:0] state;
reg outp;
always @( posedge clk, rst )
begin
if( rst )
state <= 2'b00;
else
begin
case( {state,inp} )
3'b000: begin
state <= 2'b00;
outp <= 0;
end
3'b001: begin
state <= 2'b01;
outp <= 0;
end
3'b010: begin
state <= 2'b10;
outp <= 0;
end
3'b011: begin
state <= 2'b01;
outp <= 0;
end
3'b100: begin
state <= 2'b00;
outp <= 0;
end
3'b101: begin
state <= 2'b11;
outp <= 0;
end
3'b110: begin
state <= 2'b10;
outp <= 0;
end
3'b111: begin
state <= 2'b01;
outp <= 1;
end
endcase
end
end
endmodule
|
This time I combined state and inp using concatenation operator {} to make code smaller. state and inp is used together to select the case. Using this a I avoided if-begin-end-else-begin-end in every case.